1.
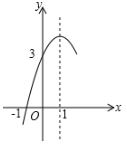
抛物线 的图象如图所示,对称轴为直线
的图象如图所示,对称轴为直线 . 下列说法:①
. 下列说法:① ;②
;② ;③
;③ (t为全体实数);④若图象上存在点
(t为全体实数);④若图象上存在点 和点
和点 , 当
, 当 时,满足
时,满足 , 则m的取值范围为
, 则m的取值范围为 . 其中正确的个数有( )
. 其中正确的个数有( )

A.
1个
B.
2个
C.
3个
D.
4个
【考点】
二次函数的最值;
二次函数y=ax²+bx+c的图象;
二次函数y=ax²+bx+c的性质;