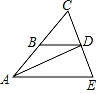
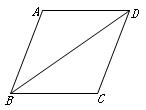
如图， AC平分∠BAD ，且交BF于点C ， BD平分∠ABC ，且交AE于点D ，连接CD ．求证：四边形ABCD是菱形．

0 返回出卷网首页

1. 如图 $\text{[math]}$ ， AC平分∠BAD ，且交BF于点C ， BD平分∠ABC ，且交AE于点D ，连接CD ．求证：四边形ABCD是菱形．

【考点】

平行线的性质; 菱形的判定; 角平分线的概念;

【答案】

您现在未登录，无法查看试题答案与解析。登录

证明题普通

1. 如图， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ .求证：四边形 $\text{[math]}$ 是菱形.

证明题容易

2. 已知：如图，B、D分别在AC、CE上，AD是∠CAE的平分线，BD∥AE，AB＝BC．

求证：AC＝AE．

证明题容易

3. 如图，▱ABCD中对角线BD平分∠ABC.

求证：▱ABCD是菱形.

证明题容易