（科技成就）随着技术的发展，为扩大网络信号的辐射范围，某通信公司在一座坡度为的小山坡上新建了一座大型的网络信号发射塔（如图所示），信号塔底端Q到坡底A的距离为米．同时为了提醒市民，在距离斜坡底A点4.4米的水平地面上立了一块警示牌，当太阳光线与水平线成角时，测得信号塔落在警示牌上的影子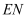长为3米．求信号塔的高．（结果精确到0.1米，参考数据：，，）

0 返回出卷网首页

1. （科技成就）随着 $\text{[math]}$ 技术的发展，为扩大网络信号的辐射范围，某通信公司在一座坡度为 $\text{[math]}$ 的小山坡 $\text{[math]}$ 上新建了一座大型的网络信号发射塔 $\text{[math]}$ （如图所示），信号塔底端Q到坡底A的距离为 $\text{[math]}$ 米．同时为了提醒市民，在距离斜坡底A点4.4米的水平地面上立了一块警示牌 $\text{[math]}$ ，当太阳光线与水平线成 $\text{[math]}$ 角时，测得信号塔 $\text{[math]}$ 落在警示牌上的影子 $\text{[math]}$ 长为3米．求信号塔 $\text{[math]}$ 的高．（结果精确到0.1米，参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

【考点】

勾股定理; 矩形的判定与性质; 解直角三角形的实际应用﹣坡度坡角问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，某人从山脚下的点A走了 $\text{[math]}$ 后到达山顶的点B，已知点B到山脚的垂直距离为 $\text{[math]}$ ，求山的坡度（ $\text{[math]}$ ，结果精确到0.001）．

解答题容易

2. 已知一段公路的坡度为 $\text{[math]}$ ，沿着这条公路每前进 $\text{[math]}$ 所上升的高度为 $\text{[math]}$ ．

填空题容易

3. 明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》：“平地秋千未起，踏板一尺离地．送行二步恰竿齐，五尺板高离地…”翻译成现代文为：如图，秋千 $\text{[math]}$ 静止的时候，踏板离地高一尺（ $\text{[math]}$ 尺），将它往前推进两步（ $\text{[math]}$ 尺），此时踏板升高离地五尺（ $\text{[math]}$ 尺），求秋千绳索（ $\text{[math]}$ 或 $\text{[math]}$ ）的长度．

综合题容易