1.
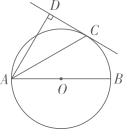
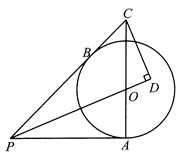
《数书九章》是宋代数学家秦九韶编写的一部实用数学大全.数学课上同学们对“遥度圆城”问题进行了改编如下:如图,一座圆形城池有正东、正南、正西和正北四个门,北门外正北方向有一棵大树,假设某人从南门向东走 里恰好可以看到这棵大树,此时转身向树的方向继续走
里恰好可以看到这棵大树,此时转身向树的方向继续走 里到达树下,则该城池的外围直径为( )
里到达树下,则该城池的外围直径为( )

A.
 里
B.
里
B.
 里
C.
里
C.
 里
D.
里
D.
 里
里
【考点】
勾股定理;
切线的性质;
相似三角形的判定与性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练