1.
阅读并理解下面内容,解答问题.
三角形的内心
定义:三角形的三条内角平分线相交于一点,这个点叫做三角形的内心.
如图1,已知AM,BN,CP是△ABC的三条内角平分线.
求证:AM,BN,CP相交于一点.
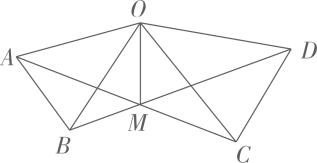
证明:如图2,设AM,BN相交于点O,
过点O分别作 ,
,
, 垂足分别为点D,E,F.
∵点O是∠BAC的平分线AM上的一点,
∴ , (依据1)
同理, .
∴ . (依据2)
∵CP是∠ACB的平分线,
∴点O在CP上,(依据3)
∴AM,BN,CP相交于一点.
请解答以下问题:
(1)上述证明过程中的“依据1”“依据2”“依据3”分别是指什么?
(2)如果 ,
,
,
, 请直接用a,b,c,r表示△ABC的面积.


【考点】
角平分线的性质;
角平分线的判定;
基础巩固
能力提升
变式训练
拓展培优
真题演练