1.
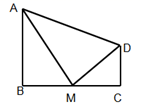
已知:如图,∠B =∠C=90°,AM是∠BAD的平分线,且M是BC的中点.
求证:DM平分∠ADC.
【考点】
角平分线的性质;
角平分线的判定;