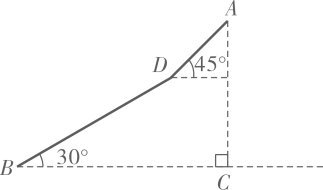
1.
古塔,是中国千年文明史的载体之一,为城市山林增光添彩.如图,为测量一座古塔的高度 , 一架遥控无人机飞到点
, 一架遥控无人机飞到点 处测得到古塔顶部
处测得到古塔顶部 的仰角为
的仰角为 , 到其底部
, 到其底部 处的俯角为
处的俯角为 , 到
, 到 处的距离为
处的距离为 . 试求出该古塔的高度
. 试求出该古塔的高度 . (结果可保留根式)
. (结果可保留根式)

【考点】
含30°角的直角三角形;
解直角三角形的实际应用﹣仰角俯角问题;
基础巩固
能力提升
变式训练
拓展培优
真题演练