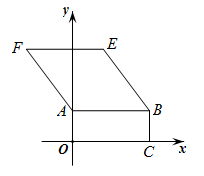
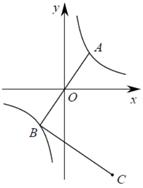
【发现问题】城市的许多街道是相互垂直或平行的，因此往往不能沿直线行走到目的地，只能按直角拐弯的方式行走．我们可以按照街道的垂直和平行方向建立平面直角坐标系，对两点和，用以下方式定义两点间的“折线距离”：．（1）①已知点，则______；②函数的图象如图1，是图象上一点，若，则点的坐标为______；（2）如图2，菱形顶点的坐标是，，．小明发现：菱形的边上会有两个点分别到原点的距离相等．若点在菱形的边上且，指出点在菱形的那条边上，并求出它的坐标．【拓展运用】（3）函数和函数的图象如图3，是函数图象上一点，是函数图象上一点，当和分别取到最小值时，求的值．

0 返回出卷网首页

1. 【发现问题】城市的许多街道是相互垂直或平行的，因此往往不能沿直线行走到目的地，只能按直角拐弯的方式行走．我们可以按照街道的垂直和平行方向建立平面直角坐标系 $\text{[math]}$ ，对两点 $\text{[math]}$ 和 $\text{[math]}$ ，用以下方式定义两点间的“折线距离”： $\text{[math]}$ ．

（1）①已知点 $\text{[math]}$ ，则 $\text{[math]}$ ______；

②函数 $\text{[math]}$ 的图象如图1， $\text{[math]}$ 是图象上一点，若 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标为______；

（2）如图2，菱形 $\text{[math]}$ 顶点 $\text{[math]}$ 的坐标是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．小明发现：菱形 $\text{[math]}$ 的边上会有两个点分别到原点 $\text{[math]}$ 的距离 $\text{[math]}$ 相等．若点 $\text{[math]}$ 在菱形的边上且 $\text{[math]}$ ，指出点 $\text{[math]}$ 在菱形的那条边上，并求出它的坐标．

【拓展运用】

（3）函数 $\text{[math]}$ 和函数 $\text{[math]}$ 的图象如图3， $\text{[math]}$ 是函数 $\text{[math]}$ 图象上一点， $\text{[math]}$ 是函数 $\text{[math]}$ 图象上一点，当 $\text{[math]}$ 和 $\text{[math]}$ 分别取到最小值时，求 $\text{[math]}$ 的值．