1.
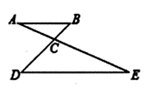
【感知】如图①,在 中,点D、E在边
中,点D、E在边 上,连接
上,连接 , 若
, 若
 , 则
, 则  度;
度;
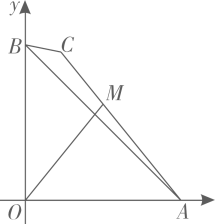
【探究】如图②,在中,点D、E分别在边
上,连接
, 若
, 求
的度数;
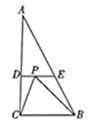
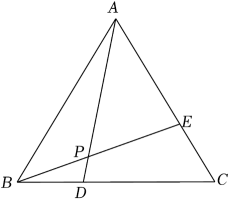
【应用】如图③,在中,点E在边
上,点D、F在边
上,连接
、
, 且
,
,
, 则
= .

【考点】
勾股定理;
相似三角形的判定与性质;
三角形全等的判定-SAS;