一、选择题(共12题,共36分)
8.
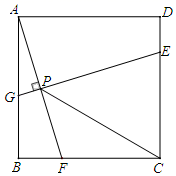
(2024八下·农安期末)如图,有一个边长为 的正方形
的正方形 , 将一块
, 将一块 的三角板直角顶点与正方形对角线交点O重合,两条直角边分别与
的三角板直角顶点与正方形对角线交点O重合,两条直角边分别与 边交于点E,与
边交于点E,与 边交于点F.则四边形
边交于点F.则四边形 的面积是( )
的面积是( )

A.
 B.
B.
 C.
C.
 D.
D.

二、填空题(共6题,共18分)