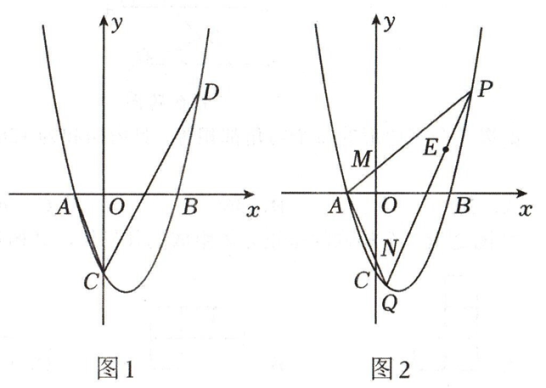
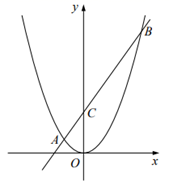
如图，在平面直角坐标系中，O为坐标原点，点C为y轴正半轴上的一个动点，过点C的直线与二次函数的图象交于A、B两点，且，P为的中点，设点P的坐标为，写出y关于x的函数表达式为：.

0 返回出卷网首页

1. 如图，在平面直角坐标系中，O为坐标原点，点C为y轴正半轴上的一个动点，过点C的直线与二次函数 $\text{[math]}$ 的图象交于A、B两点，且 $\text{[math]}$ ，P为 $\text{[math]}$ 的中点，设点P的坐标为 $\text{[math]}$ ，写出y关于x的函数表达式为：.

【考点】

相似三角形的判定与性质; 二次函数与一次函数的综合应用; 二次函数图象上点的坐标特征;

【答案】

您现在未登录，无法查看试题答案与解析。登录

填空题普通

1. 如图， $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长度为.

填空题容易

2. 如图，在 $\text{[math]}$ 中，D是 $\text{[math]}$ 边上的点，以点D为顶点作 $\text{[math]}$ ，使 $\text{[math]}$ ， $\text{[math]}$ 交边 $\text{[math]}$ 于点E．假设 $\text{[math]}$ ，那么 $\text{[math]}$ ．

填空题容易

3. 如图，△ABC中，点D、E分别在AB、AC上，DE∥BC，AD：DB＝1：2，则△ADE与△ABC的面积的比为．

填空题容易