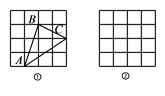图①、图②、图③均是的正方形网格，每个小正方形的顶点称为格点，线段的端点均在格点上．在图①、图②、图③中以为边各画一个等腰三角形，使其依次为锐角三角形、直角三角形、钝角三角形，且所画三角形的顶点均在格点上．

0 返回出卷网首页

1. 图①、图②、图③均是 $\text{[math]}$ 的正方形网格，每个小正方形的顶点称为格点，线段 $\text{[math]}$ 的端点均在格点上．在图①、图②、图③中以 $\text{[math]}$ 为边各画一个等腰三角形，使其依次为锐角三角形、直角三角形、钝角三角形，且所画三角形的顶点均在格点上．

【考点】

等腰三角形的性质; 勾股定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

作图题普通

1. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的平分线．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为．

填空题容易

2. 如图，已知Rt△ABC中，∠C=90°，∠BAC=45°，用尺规作图：在AC的延长线上截取AD=AB，并连接BD（不写作法，保留作图痕迹），求∠BDC的度数。

作图题容易