1.
二次函数y=﹣ x2+bx+c的图象与直线y=﹣
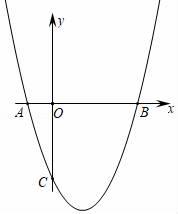
x2+bx+c的图象与直线y=﹣ x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为C(﹣3,0).
x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为C(﹣3,0).
(1)填空:b=_____ , c=_____.
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(3)在(2)的条件下,点N在何位置时,BM与NC相互垂直平分?并求出所有满足条件的N点的坐标.

【考点】
待定系数法求二次函数解析式;
二次函数-线段周长问题;
基础巩固
能力提升
变式训练
拓展培优